ALEKS Trigonometry
This flashcard set explains essential angle-related concepts in trigonometry, including definitions of initial and terminal sides, direction of angle rotation (positive vs. negative), and the concept of coterminal angles. It’s perfect for mastering the basics of angle measurement and rotation.
Terminal vs initial side
define Angle
initial - Ray that the rotation starts on
terminal - Ray that the rotation ends on
The distance of that rotation about the vertex of the rays
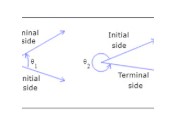
Key Terms
Terminal vs initial side
define Angle
initial - Ray that the rotation starts on
terminal - Ray that the rotation ends on
The distance of that rotation about the vertex...
Positive vs negative angle
If the rotation moves clockwise, the angle will be negative
Counter clockwise, positive angle
Where does an angle have to "stop"
It does,t it can rotate past a full revolution
Define coterminal angles
Angles that share the same terminal side, but no necessarily the same initial side
How many radians is a 360 degree revolution
2π
How many radians is 1/4 of a revolution?
1/3?
2π/4 = π/2
2π/3
Related Flashcard Decks
Study Tips
- Press F to enter focus mode for distraction-free studying
- Review cards regularly to improve retention
- Try to recall the answer before flipping the card
- Share this deck with friends to study together
| Term | Definition |
|---|---|
Terminal vs initial side | initial - Ray that the rotation starts on |
Positive vs negative angle | If the rotation moves clockwise, the angle will be negative |
Where does an angle have to "stop" | It does,t it can rotate past a full revolution |
Define coterminal angles | Angles that share the same terminal side, but no necessarily the same initial side |
How many radians is a 360 degree revolution | 2π |
How many radians is 1/4 of a revolution? | 2π/4 = π/2 |
Define standard position of an angle | vertex at origin and initial side long positive X axis |
Quadrantal Angle | Angles (in std. Position) whose terminal sides coincide with one of the coordinate axes |
reference angles | the acute angle formed by the terminal side of an angle in standard position and the x-axis |
trig ratios mnumonicn | soh cah toa |
Which of sine, cosine, or tagent is represented by the (x,y) coordinates where the terminal angle intersects the unit circle | (cos,sin) |
Unit circle, MEMORIZE IT | |
MAGIC HEXEGON | |
using trigonometric ratios to find unknown angle in a right triangle given length of two sides | use soh cah toa |
Finding three of the 6 trig. identities given two sides | 1. use pethag. theorem to find the third side |
Steps to solve right triangles given one side and an angle | To find unknown angle: |
ALL TRIG IDENTITIES | |
When finding csc, sec, or cot of a xpi/y form angle, do you flip the numerator and denominator? | NO, you put it all under 1 |
1/(sqrt(2)/2) = ? | sqrt(2), why? |
1/(1/2) = | How many halves in one whole? |
(1/2)/(sqrt(3)/2) = | sqrt(3)/3 |
Finding coterminal within a given range of angles for a given angle | To get a coterminal angle you add or subtract a multiple of 2π or 360⁰, this places the terminal side back at that location, though the angle size is different. |
How is 17pi/12 between 0 and 2pi | because 1 pi is divided into 12 pieces, so 24 would be 2pi |
How is 3pi/2 between 0 and 2pi | 4pi/2 is 2pi |
Finding the reference angle for a given radian angle | The reference angle of a given angle will be that angle minus either pi/2, pi, 3pi/2, or 2pi depending on which quadrant the angle is in. |
law of sine, finding sides and angles of a non-right triangle when given some sides and angles | |
Arc length and central angle measure | s = rθ |
Arc length and central angle measure (cont) | When you divide s by r, that gives you the radian fraction |
How to convert from radians to degrees | Radian * 180/pi |
The hypotenus of a right triangle begins on the origin but has a point (x,y) on the terminal side that lies outside the unit circle. | |
Finding values of trigonometric functions given information about an angle: Point on the terminal angle Not in the unit circle | Given that r = sqrt(x^2+y^2), you can calculate the hypotenus (r) with the given point. |