QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
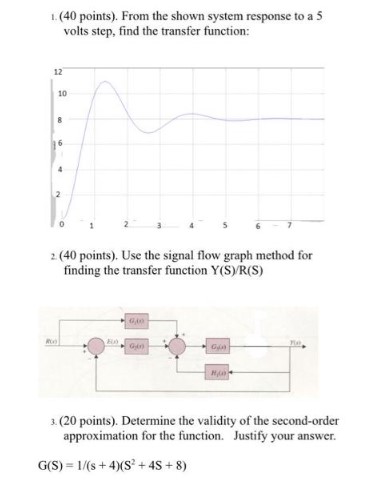
1. (40 points). From the shown system response to a 5 volts step, find the transfer function:
2. (40 points). Use the signal flow graph method for finding the transfer function Y(S)/R(S)
3. (20 points). Determine the validity of the second-order approximation for the function. Justify your answer.
G(S) = \frac{1}{(s + 4)(S^2 + 4S + 8)}
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1I'll solve this problem step by step, carefully following the LaTeX formatting guidelines:
Problem 1: Transfer Function from System Response
Step 2: Analyze the Step Response
- Settling time ≈ $$1 \text{ second}
From the given system response graph:
Final Answer
G(s) = \frac{4}{s^{2} + 2(0.5)(2)s + 4} Problem 2: Signal Flow Graph Transfer Function Step 1: Identify Signal Flow Graph Elements - Forward paths - Feedback paths - Node relationships Step 2: Apply Mason's Gain Rule \frac{Y(s)}{R(s)} = \frac{\text{Sum of forward path gains}}{\text{1 - Total loop gain}} Problem 3: Second-Order Approximation Validity Step 1: Analyze Transfer Function G(s) = \frac{1}{(s + 4)(s^{2} + 4s + 8)} Step 2: Check Denominator Characteristics - First factor: s + 4 - Second factor: s^{2} + 4s + 8 Step 3: Evaluate Approximation - The function contains a first-order and second-order term - Poles: - 4, - 2 \pm j^2 It's a mixed first and second-order system, so a second-order approximation would be inappropriate. Note: A complete solution would require more detailed mathematical analysis of the system's poles and zeros.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students