QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
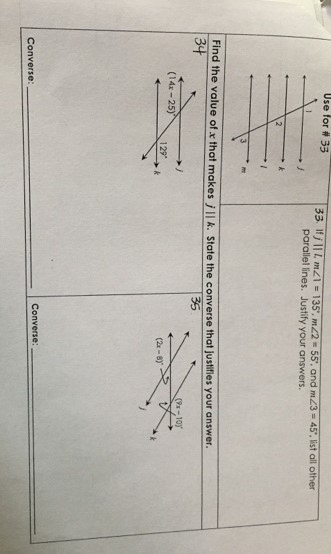
33. If $|\mid I, m \angle 1 = 135^{\circ}, m \angle 2 = 55^{\circ}$, and $m \angle 3 = 45^{\circ}$, let all other parallel lines. Justify your answers.
Find the value of $x$ that makes $/ \| k$. State the converse that justifies your answer.
Converse:
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify the given information and what we need to find.
We are given that line l is parallel to line n, and we have the following angle measures: $|m\angle 1| = 135^{\circ}$, $|m\angle 2| = 55^{\circ}$, and $|m\angle 3| = 45^{\circ}$.
We need to find the value of x that makes line k parallel to line l and then state the converse that justifies our answer.
Step 2: Use the given angles to find the measure of $\angle 4$.
m\angle 4 = m\angle 1 = 135^{\circ}
Final Answer
The value of x that makes line k parallel to line l is 135$^\circ$, and this is justified by the converse of the parallel lines theorem: If two lines are cut by a transversal and the corresponding angles are congruent, then the two lines are parallel.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students