QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
5. 定义 $f(0,0)$ 的值, 使 $f$ 在原点连续. Define $f(0,0)$ in a way that extends $f$ to be continuous at the origin.
f(x, y)=\ln \left(\frac{3 x^{2}-x^{2} y^{2}+ 3 y^{2}}{x^{2}+y^{2}}\right)
# 2.2. 位移数, Partial Derivatives
Attachments
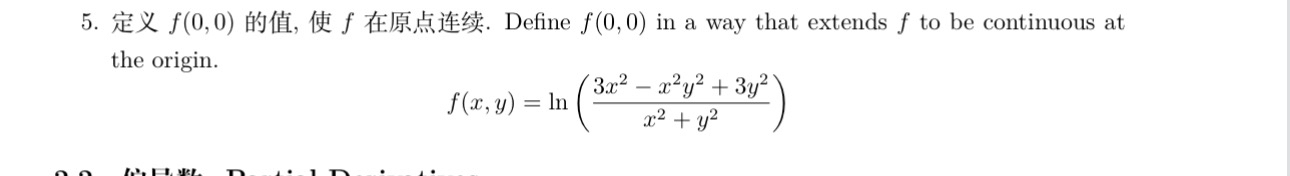
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1**Homework Problem: Define $f(0,0)$ in a way that extends $f$ to be continuous at the origin.**
Hence, $f(x,y)$ is continuous at the origin.
Then, Then, However, we should verify that this definition does not create a discontinuity at the origin. Then, Thus, we define Therefore, we require \lim\_{x\to 0} x^2 g(x,mx) = 0 In this case, the limit becomes Therefore, we define **
Final Answer
Define $f(0,0) = \ln(3)$. Then, for $(x,y) \neq (0,0)$, let f(x,y) = \ln\left(\frac{3x^2 -x^2 y^2 + 3y^2 +x^3 y}{x^2 +y^2}\right) With this definition, $f(x,y)$ is continuous at the origin.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students