QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
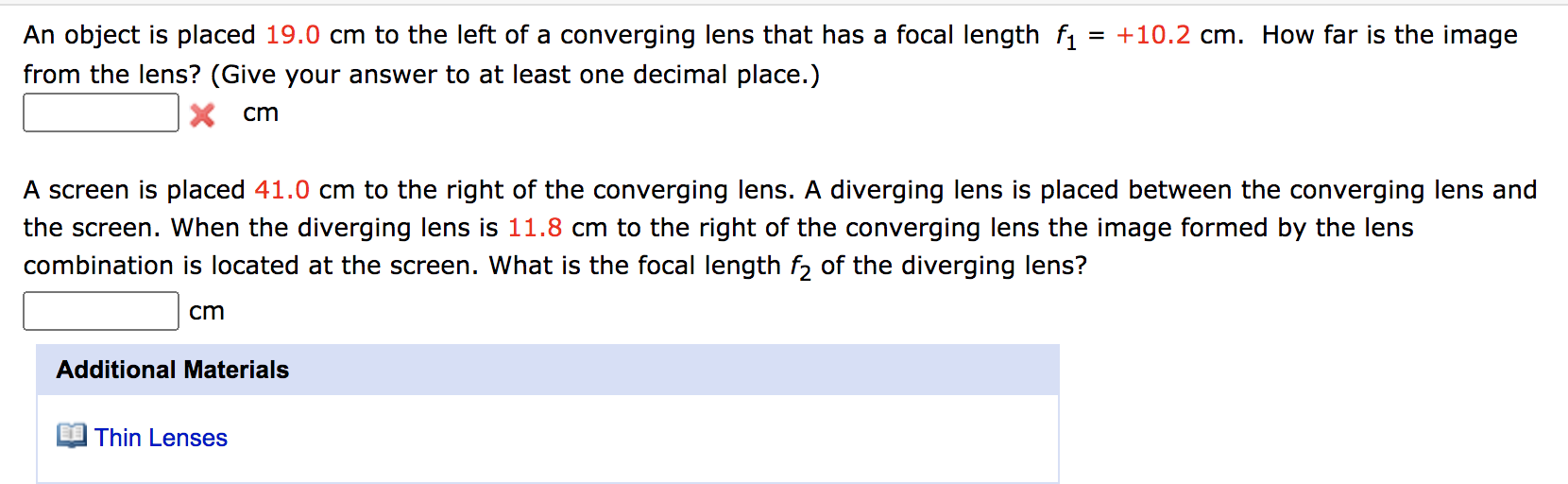
An object is placed 19.0 cm to the left of a converging lens that has a focal length f_1 = + 10.2 cm. How far is the image from the lens? (Give your answer to at least one decimal place.)
A screen is placed 41.0 cm to the right of the converging lens. A diverging lens is placed between the converging lens and the screen. When the diverging lens is 11.8 cm to the right of the converging lens the image formed by the lens combination is located at the screen. What is the focal length f_2 of the diverging lens?
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Use the thin lens equation to find the image distance (d_i) for the converging lens.
d_i = \frac{f_1 \times d_o}{d_o - f_1}
The thin lens equation is given by:
Step 2: Plug in the given values and calculate the image distance for the converging lens.
d_i = \frac{(+10.2 \ \text{cm}) \times (19.0 \ \text{cm})}{19.0 \ \text{cm} - 10.2 \ \text{cm}} = \boxed{30.2 \ \text{cm}}
Final Answer
The focal length of the diverging lens is f_2 = - 7.58 \ \text{cm}.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students