QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
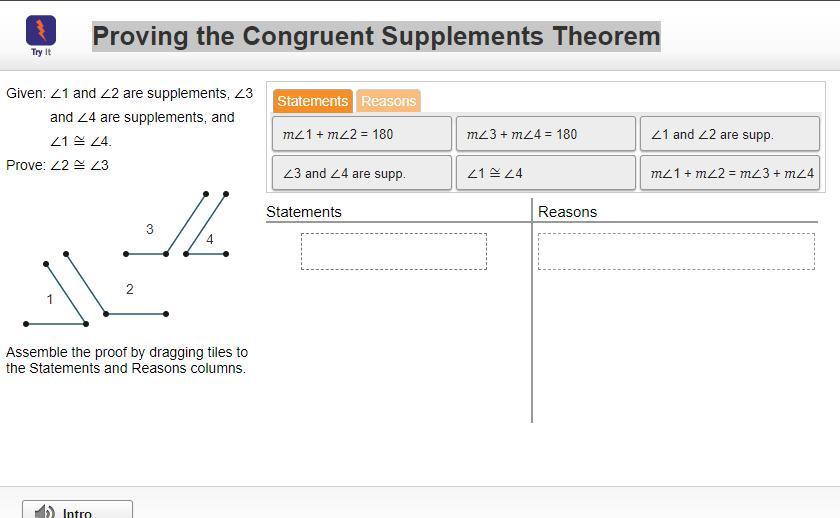
# Proving the Congruent Supplements Theorem
Given: $\angle 1$ and $\angle 2$ are supplements, $\angle 3$ and $\angle 4$ are supplements, and $\angle 1 \cong \angle 4$. Prove: $\angle 2 \cong \angle 3$
| Statements | Reasons | |
| --- | --- | --- |
| $m \angle 1 +m \angle 2 = 180$ | $m \angle 3 +m \angle 4 = 180$ | $\angle 1$ and $\angle 2$ are supp. |
| $\angle 3$ and $\angle 4$ are supp. | $\angle 1 \cong \angle 4$ | $m \angle 1 +m \angle 2 =m \angle 3 +m \angle 4$ |
Assemble the proof by dragging tiles to the Statements and Reasons columns.
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1I'll solve this proof step by step using proper LaTeX formatting:
Step 2: Understand the Given Information
- $$\angle 1 \cong \angle 4
- \angle 3 and \angle 4 are supplements
Final Answer
\angle 2 \cong \angle 3 is proven.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students