QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
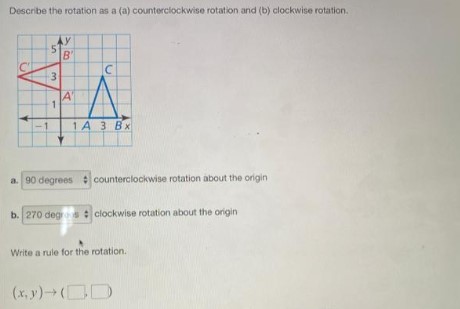
Describe the rotation as a (a) counterclockwise rotation and (b) clockwise rotation.
a. 90 degrees ↑ counterclockwise rotation about the origin
b. 270 degrees ↑ clockwise rotation about the origin
Write a rule for the rotation.
(x, y) \rightarrow (\square, \square)
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1I'll solve this step by step using the precise LaTeX formatting guidelines:
Step 2: Counterclockwise 90 -degree Rotation
\begin{cases}
For a 90 -degree counterclockwise rotation about the origin, the general transformation rule is: x' = -y \ y' = x \end{cases} This means: - The x-coordinate becomes the negative of the original y-coordinate - The y-coordinate becomes the original x-coordinate
Final Answer
- Counterclockwise 90 -degree rotation: (x, y) \rightarrow (-y, x) - Clockwise 270 -degree rotation: (x, y) \rightarrow (-y, x) Note: Both rotations result in the same coordinate transformation due to the symmetry of 90 -degree rotations.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students