QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
Directions: Complete each proof.
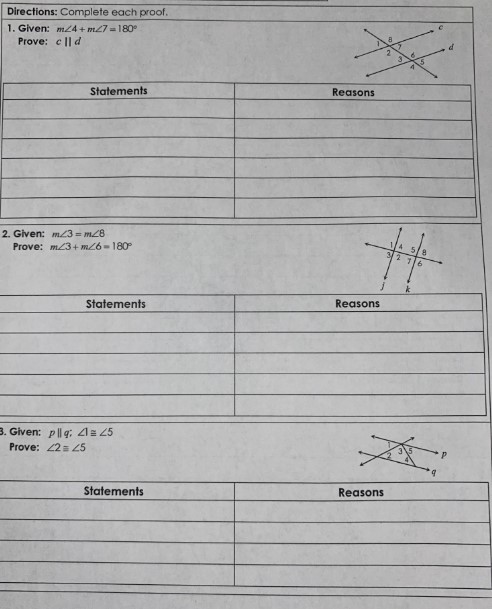
1. Given: $m \angle 4 +m \angle 7 = 180^{\circ}$
Prove: $c\|d$
| Statements | Reasons |
| :-- | :-- |
| | |
| | |
| | |
| | |
| | |
2. Given: $m \angle 3 =m \angle 8$
Prove: $m \angle 3 +m \angle 6 = 180^{\circ}$
| Statements | Reasons |
| :-- | :-- |
| | |
| | |
| | |
3. Given: $p \| q: \angle 1 \cong \angle 5$
Prove: $\angle 2 \cong \angle 5$
| Statements | Reasons |
| :-- | :-- |
| | |
| | |
| | |
| | |
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1
| $c || d$ | Converse of the Same Side Interior Angles Theorem |
Prove: $c || d$ | Statements | Reasons | | :-- | :-- |
Step 2
| $m angle 3 + m angle 9 = 180^{\circ}$ | Linear pair postulate |
Prove: $m angle 3 + m angle 6 = 180^{\circ}$ | Statements | Reasons | | :-- | :-- |
Final Answer
| $∠ 2 ≅ ∠ 1$ | Transitive property of congruence |
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students