QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
**Triangle Inequality Theorem 1 (Ss → Aa)** – if one side of a triangle is longer than the second, then the angle opposite the longer side is larger than the angle opposite the second side.
**Example:** Figure 1 shows a triangle with sides of different measures. List all angles of figure 1 in ascending order.
*Figure 1 *
**Solution:**
By the Triangle inequality theorem 1, **MN** is the longest side and **xP**, the angle opposite **MN** is the largest angle. Also, since **MP** is the shortest side then **xp**, the angle opposite **MP** is the smallest angle. Hence, **xNxMxP**.
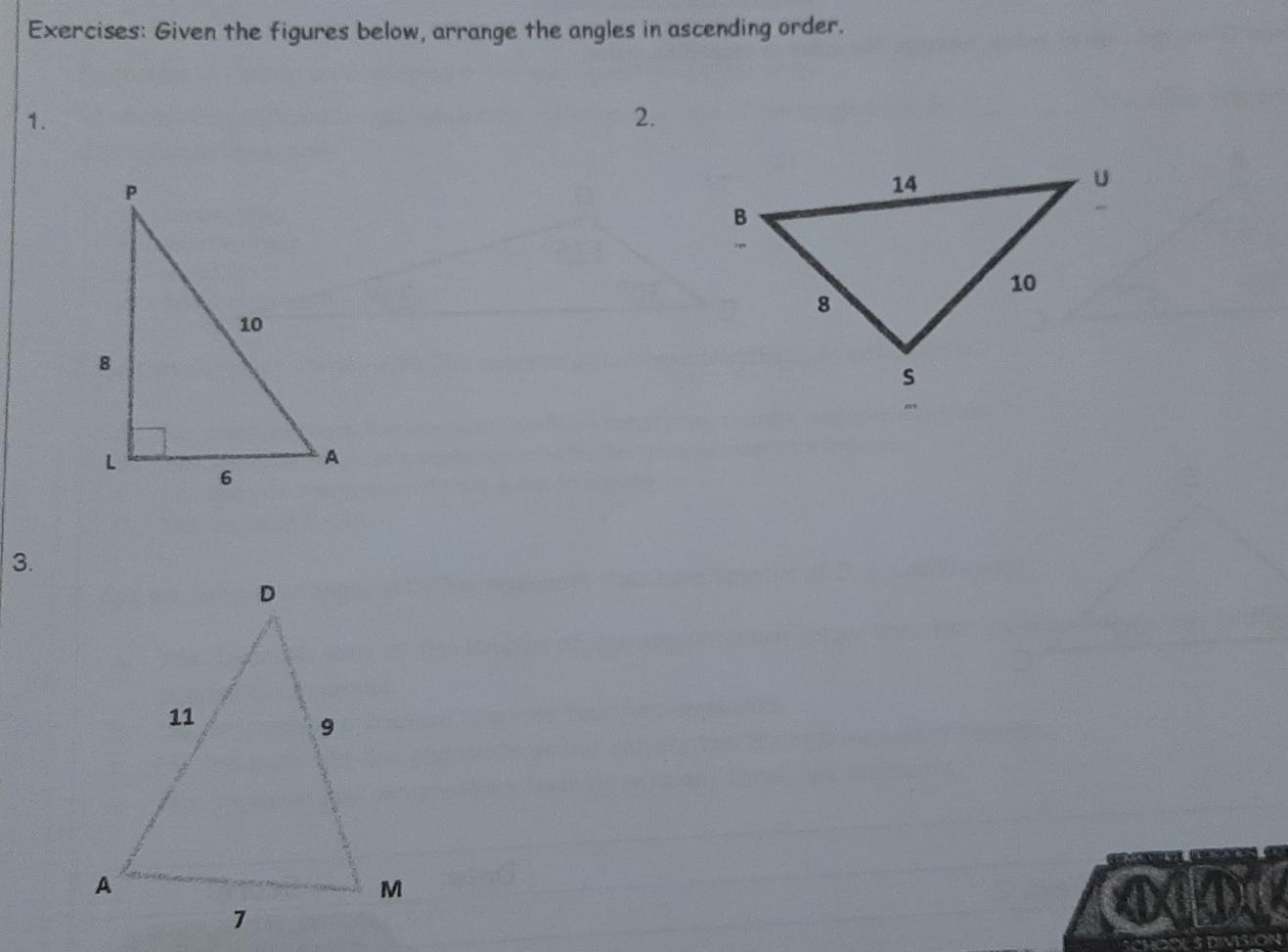
Exercises: Given the figures below, arrange the angles in ascending order.
1.
2.
3.
Attachments

6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify the longest side and the smallest side in each triangle.
In Triangle 1: - The longest side is **MN** since, by the Triangle Inequality Theorem 1, if one side of a triangle is longer than the second, then the angle opposite the longer side is larger than the angle opposite the second side. Here, side **MN** is longer than sides **MP** and **NP**. - The smallest side is **MP**. In Triangle 2: - The longest side is **XY** since it is longer than side **XZ**. - The smallest side is **XZ**. In Triangle 3: - The longest side is **PQ** since it is longer than side **PR**. - The smallest side is **PR**.
Step 2: Identify the angles opposite the longest and smallest sides.
In Triangle 1: - The angle opposite the longest side **MN** is **x**. - The angle opposite the smallest side **MP** is **xp**. In Triangle 2: - The angle opposite the longest side **XY** is **α**. - The angle opposite the smallest side **XZ** is **xz**. In Triangle 3: - The angle opposite the longest side **PQ** is **θ**. - The angle opposite the smallest side **PR** is **pr**.
Final Answer
1. Triangle 1: xp < xN < xM 2. Triangle 2: xz < α < β 3. Triangle 3: pr < pr + θ
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students