QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
What is the recursive formula for this geometric sequence? $- 4,- 24,- 144,- 864, \ldots$
O A. $\left\{\begin{array}{l}a_{1}=- 4 \\ a_{n}=a_{n- 1} \bullet 6\end{array}\right.$
O B. $\left\{\begin{array}{l}a_{1}=- 6 \\ a_{n}=a_{n- 1} \bullet 30\end{array}\right.$
O C. $\left\{\begin{array}{l}a_{1}=- 4 \\ a_{n}=a_{n- 1} \bullet 30\end{array}\right.$
O D. $\left\{\begin{array}{l}a_{1}=- 6 \\ a_{n}=a_{n- 1} \bullet 4\end{array}\right.$
Attachments
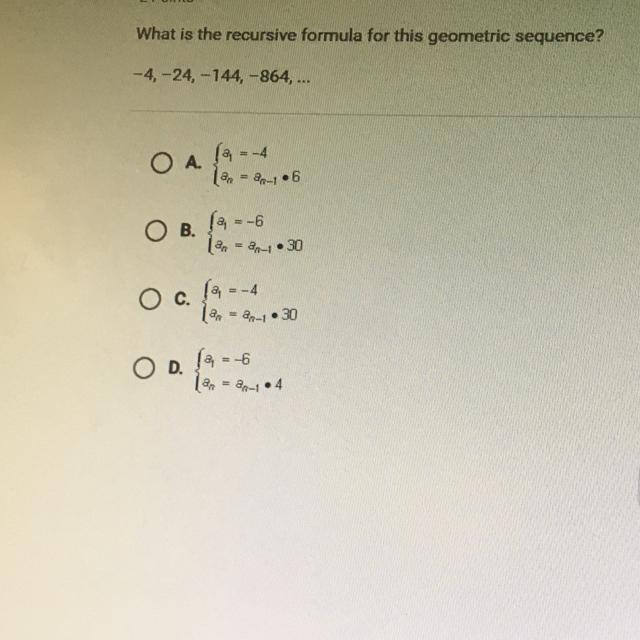
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1Let's solve this step by step:
Step 2: Identify the first term and the common ratio
\frac{-864}{-144} = 6
- Let's find the common ratio by dividing consecutive terms:
Final Answer
Option A is the correct recursive formula for this geometric sequence.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students