QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
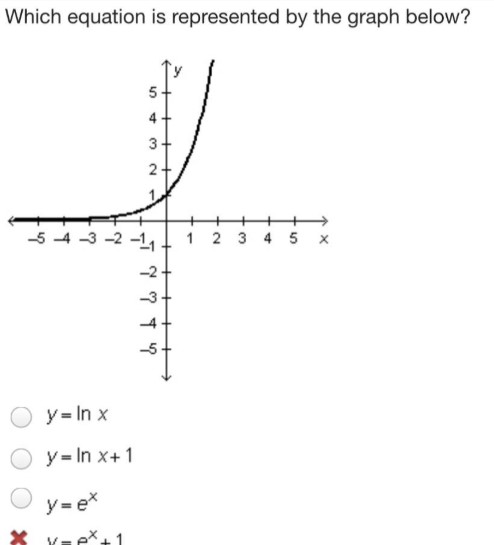
Which equation is represented by the graph below?
$y=\ln x$
$y=\ln x+ 1$
$y=e^{x}$
$x=e^{x}+ 1$
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify the shape of the graph
This type of graph is represented by the equation $y = ae^{bx}$, where a and b are constants.
The given graph is an exponential curve that increases as x increases. However, the given options do not include this form. We need to find a transformation of this form that matches one of the given options.
Step 2: Identify the asymptote
However, the given graph is not a reflection of $y = \ln x$ about the x-axis, so it cannot be $y = -\ln x$.
The exponential curve approaches the x-axis as x approaches negative infinity. This means that the x-axis is the horizontal asymptote of the curve.
Final Answer
The equation represented by the graph is $y = \ln x + 1$.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students