QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
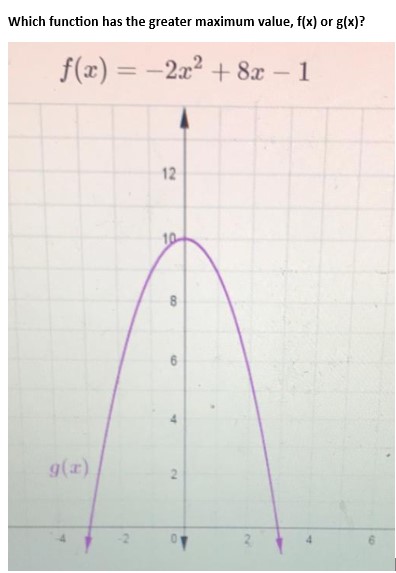
Which function has the greater maximum value, f(x) or g(x)?
f(x) = - 2x^2 + 8x - 1
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify the maximum value of each function
For $$f(x) = -2x^2 + 8x - 1$$, we have $$a = -2$$, $$h = 4$$, and $$k = -33$$.
To compare the maximum values of the two functions, we first need to find the maximum value of each function. Since both functions are quadratic functions, we can find their maximum values by completing the square or using the formula for the maximum value of a quadratic function.
Step 2: Find the maximum value of f(x)
So, the maximum value of $$f(x) = -2x^2 + 8x - 1$$ is $$-33$$.
Using the formula for the maximum value of a quadratic function, we have:
Final Answer
The maximum value of g(x) is greater than the maximum value of f(x).
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students