QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
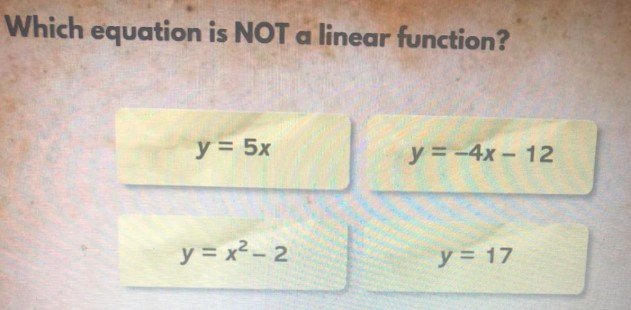
# Which equation is NOT a linear function?
\begin{gathered}
y= 5 x \\
y=x^{2}- 2
\end{gathered}
y=- 4 x- 12
y= 17
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify the equations provided and understand what it means for an equation to be a linear function.
An equation is a linear function if it is in the form y = mx + b, where m and b are constants. The equation can also be written in the form f(2$) = mx + b.
Step 2: Examine each equation to determine if it is a linear function.
Equation 1: y = 5x This equation is in the form y = mx + b, where m = 5 and b = 0. Therefore, it is a linear function. Equation 2: y = x^2 - 2 This equation is a quadratic function, not a linear function, because of the x^2 term. Equation 3: y = - 4x - 12 This equation is in the form y = mx + b, where m = - 4 and b = - 12. Therefore, it is a linear function. Equation 4: y = 17 This equation is a constant function, which is a type of linear function. It can be written in the form y = mx + b, where m = 0 and b = 17.
Final Answer
The equation y = x^2 - 2 is NOT a linear function.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students