QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
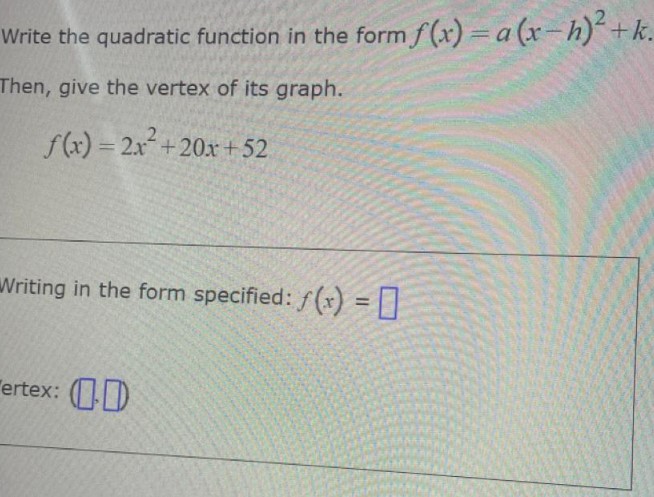
Write the quadratic function in the form $f(x)=a(x-h)^{2}+k$. Then, give the vertex of its graph.
f(x)= 2 x^{2}+ 20 x+ 52
Writing in the form specified: $f(x)=\square$
Vertex: $(\square \square)$
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify the values of a, h, and k in the given quadratic function.
- $h$ and $k$ are yet to be determined.
Step 2: Completing the square to rewrite the function in the specified form.
f(2$)= 2(x+ 10 - 10)^{2}+ 52 + 2(10)^{2}- 2(10)^{2} Now, simplify the expression: f(2$)= 2(x+ 10)^{2}+ 52 + 40 - 200 f(2$)= 2(x+ 10)^{2}- 168
Final Answer
The quadratic function in the form $f(x)=a(x-h)^{2}+k$ is: f(x)= 2(x+ 10)^{2}- 168 The vertex of its graph is $(- 10, - 168)$.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students