QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
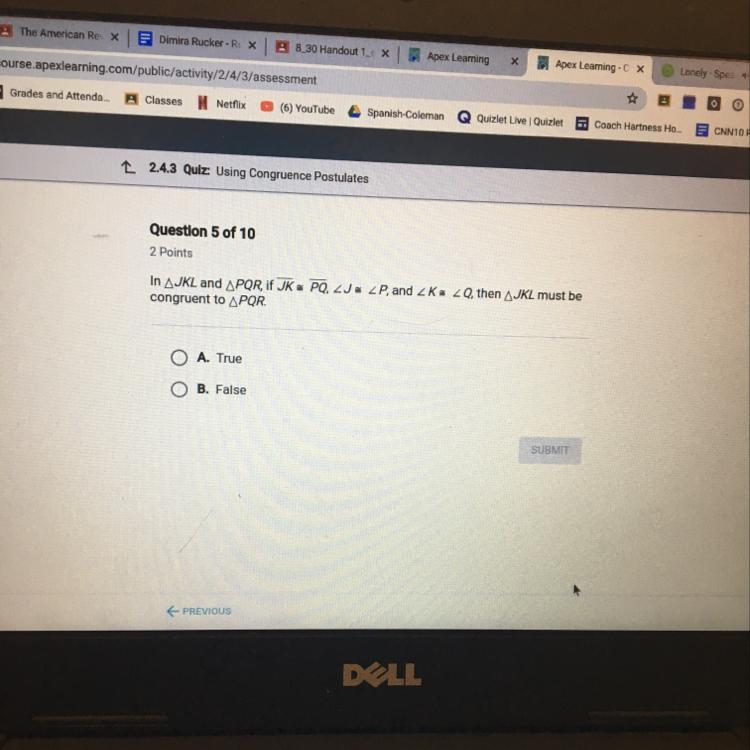
# 2.4.3 Quiz: Using Congruence Postulates
## Question 5 of 10
### 2 Points
In **△JKL** and **△PQR**, if **JK = PQ**, **LJ = LP**, and **LK = LQ**, then **△JKL** must be congruent to **△PQR**.
- **A.** True
- **B.** False
**SUBMIT**
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Analyze the given information and apply the SSS (Side-Side-Side) Congruence Postulate.
The SSS Congruence Postulate states that if three sides of one triangle are equal to the three corresponding sides of another triangle, then the two triangles are congruent. In this case, we are given that: JK = PQ (Side JK of triangle JKL corresponds to side PQ of triangle PQR) LJ = LP (Side LJ of triangle JKL corresponds to side LP of triangle PQR) LK = LQ (Side LK of triangle JKL corresponds to side LQ of triangle PQR)
Step 2: Compare the given information with the SSS Congruence Postulate conditions.
The given information matches the conditions stated in the SSS Congruence Postulate. Therefore, if JK = PQ, LJ = LP, and LK = LQ, then △JKL must be congruent to △PQR.
Final Answer
The statement is true.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students