QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
Find the simplified product where $x \geq 0: \sqrt{5 x}\left(\sqrt{8 x^{2}}- 2 \sqrt{x}\right)$
- $\sqrt{10 x}$
- $2 x \sqrt{40 x}- 2 x$
- $2 x \sqrt{10 x}- 2 \sqrt{5 x}$
- $2 x \sqrt{10 x}- 2 x \sqrt{5}$
Attachments
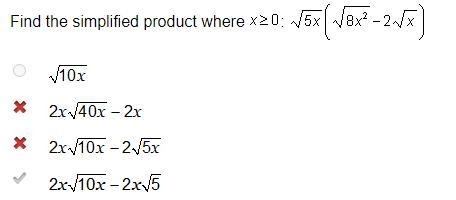
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Distribute the \sqrt{5x} inside the parentheses, being careful with the signs.
\sqrt{5x}\left(\sqrt{8x^2} - 2\sqrt{x}\right) = \sqrt{5x}\sqrt{8x^2} - \sqrt{5x} \cdot 2\sqrt{x}
Step 2: Simplify the terms on the right side of the equation.
Recall the product rule for radicals: \sqrt{a}\sqrt{b} = \sqrt{ab} \begin{align*} \sqrt{5x}\sqrt{8x^2} - \sqrt{5x} \cdot 2\sqrt{x} &= \sqrt{5x \cdot 8x^2} - 2\sqrt{5x^2} \ &= \sqrt{40x^3} - 2x\sqrt{5} \end{align*}
Final Answer
The simplified product is 2x\sqrt{10x} - 2x\sqrt{5}.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students