QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
# 2 Lessons $\odot$ Assessments $\checkmark$ Gradebook $\square$ Email Tools $\cdot$
## 4 Add Audio $\rightarrow$ Add Video
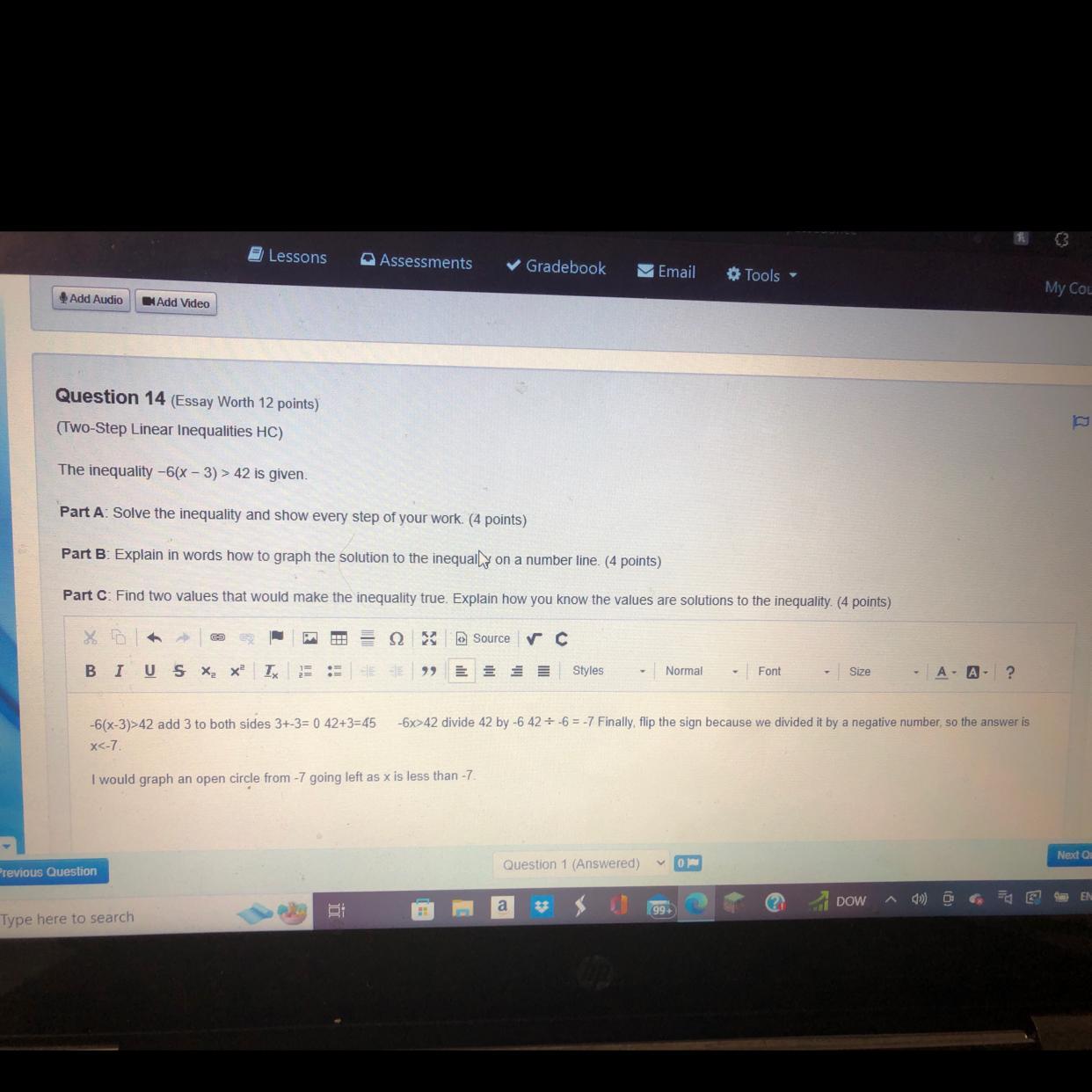
## Question 14 (Essay Worth 12 points)
## (Two-Step Linear Inequalities HC)
The inequality $- 6(x- 3)>42$ is given.
Part A: Solve the inequality and show every step of your work. (4 points)
Part B: Explain in words how to graph the solution to the inequal on a number line. (4 points)
Part C: Find two values that would make the inequality true. Explain how you know the values are solutions to the inequality. (4 points)
$- 6(x- 3)>42$ add 3 to both sides $3 +- 3 = 042 + 3 = 45 \quad- 6 x>42$ divide 42 by $- 642 \div- 6 =- 7$ Finally, flip the sign because we divided it by a negative number, so the answer is $x<- 7$.
I would graph an open circle from - 7 going left as $x$ is less than - 7 .
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Solve the inequality.
x < -7 \quad \color{blue}{\text{Simplify the right side}}
Step 2: Explain in words how to graph the solution on a number line.
The open circle indicates that $-7$ is not a solution, and the shading to the left shows that all values less than $-7$ are solutions.
Final Answer
Part A: The solution to the inequality is $x < - 1$. Part B: To graph the solution on a number line, put an open circle at $- 1$ and shade all numbers to the left. Part C: Two values that make the inequality true are $- 1$ and $- 1$.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students