QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
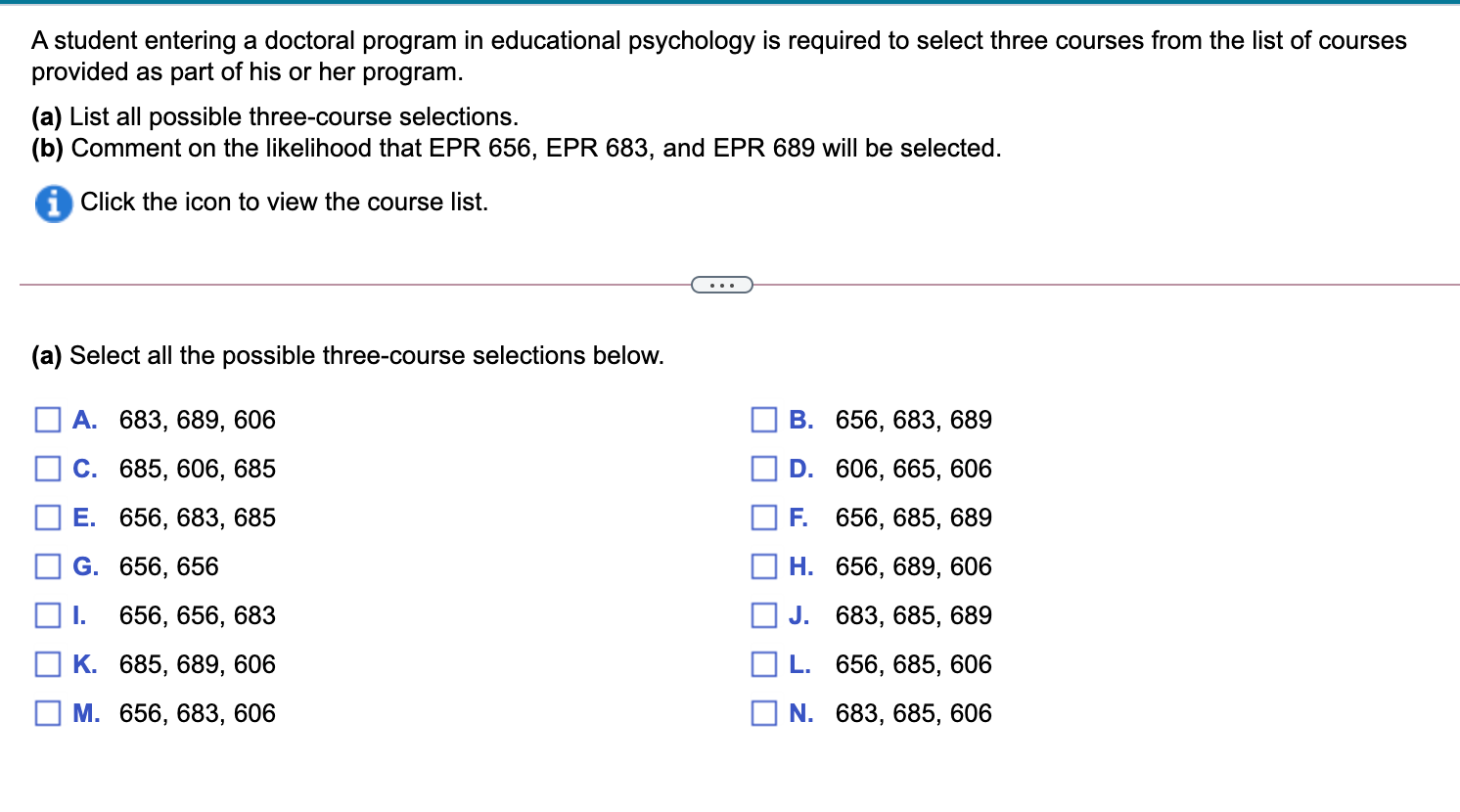
A student entering a doctoral program in educational psychology is required to select three courses from the list of courses provided as part of his or her program.
(a) List all possible three-course selections.
(b) Comment on the likelihood that EPR 656, EPR 683, and EPR 689 will be selected.
Click the icon to view the course list.
(a) Select all the possible three-course selections below.
$\square$ A. 683, 689, 606
$\square$ B. 656, 683, 689
$\square$ C. 685, 606, 685
$\square$ D. 606, 665, 606
$\square$ E. 656, 683, 685
$\square$ F. 656, 685, 689
$\square$ G. 656, 656
$\square$ H. 656, 689, 606
$\square$ I. 656, 656, 683
$\square$ J. 683, 685, 689
$\square$ K. 685, 689, 606
$\square$ L. 656, 685, 606
$\square$ M. 656, 683, 606
$\square$ N. 683, 685, 606
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify all possible unique three-course selections from the list of courses.
C(9, 3) = \frac{9!}{3!(9-3)!} = \frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{(3 \times 2 \times 1)(6 \times 5 \times 4 \times 3 \times 2 \times 1)} = 84
There are 9 courses in the list, and a doctoral student is required to select 3 courses. The number of ways to choose 3 courses out of 9 can be calculated using the combination formula: There are 84 possible unique three-course selections.
Step 2: Compare the given course selections with the calculated 84 possible unique three-course selections.
The given course selections are: A. 683, 689, 606 B. 656, 683, 689 C. 685, 606, 685 D. 606, 665, 606 E. 656, 683, 685 F. 656, 685, 689 G. 656, 656 H. 656, 689, 606 I. 656, 656, 683 J. 683, 685, 689 K. 685, 689, 606 L. 656, 685, 606 M. 656, 683, 606 N. 683, 685, 606
Final Answer
There are 84 possible unique three-course selections, and the likelihood of EPR 656, EPR 683, and EPR 689 being selected is approximately 1.19%.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students