QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
\begin{aligned}
& \frac{\sqrt{x^{5}}}{\sqrt[3]{x^{4}}}=x^{\frac{a}{b}} \\
& \text { If } \frac{\sqrt[3]{x^{4}}}{\sqrt[3]{x^{4}}}=x^{\frac{a}{b}} \text { for all positive values of } x \\
& \text { what is the value of } \frac{a}{b} \text { ? }
\end{aligned}
Attachments
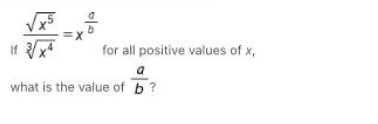
5 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify the numerator and denominator of the given equation.
The numerator is $$\sqrt{x^{5}}$$ and the denominator is $$\sqrt[3]{x^{4}}$$.
Step 2: Simplify both the numerator and the denominator.
For the denominator, we can rewrite $$\sqrt[3]{x^{4}}$$ as $$x^{\frac{4}{3}}$$.
Final Answer
The value of the ratio \frac{a}{b} is \frac{11}{3}.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students