QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
Multiply: $4 x \sqrt[3]{4 x^{2}}\left(2 \sqrt[3]{32 x^{2}}-x \sqrt[3]{2 x}\right)$
$\times 32 x^{2} \sqrt[3]{2 x}- 8 \sqrt[3]{x^{2}}$
$4 x^{2} \sqrt[3]{2 x}- 8 x^{3}$
$\times 64 x^{2} \sqrt[3]{2 x}- 8 x^{3}$
$64 x^{2} \sqrt[3]{2 x}- 8 x \sqrt[3]{x}$
Attachments
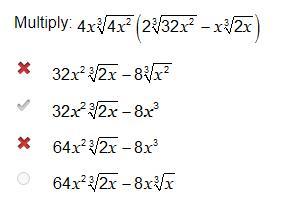
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Distribute the factor of 4x\sqrt[3]{4x^2} to each term inside the parentheses.
4x\sqrt[3]{4x^2}\times 2\sqrt[3]{32x^2} - 4x\sqrt[3]{4x^2}\times x\sqrt[3]{2x}
Step 2: Simplify the terms by multiplying the numbers and combining like radicals.
8x\left(\sqrt[3]{128x^3}\right) - 4x^2\sqrt[3]{8x^3}
Final Answer
4x\sqrt[3]{2x}\left(2 - x\right), 32x^2\sqrt[3]{2x}\left(2 - x\right)
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students