QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
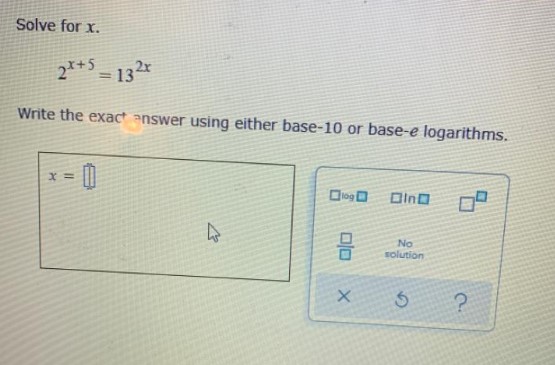
# Solve for $x$.
2^{x+ 5}= 13^{2 x}
Write the exact answer using either base- 10 or base-e logarithms.
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: To solve the equation, we will take the base- 10 logarithm (log) of both sides.
This is a valid operation since logarithms and exponentials are inverse operations. \log_{10}\left(2^{x+ 5}\right) = \log_{10}\left(13^{2x}\right)
Step 2: Using the power rule for logarithms, which states that 1$, we can rewrite the equation as:
(x+ 5)\log_{10}(2) = 2x\log_{10}(13)
Final Answer
The solution to the equation 1$.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students