QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
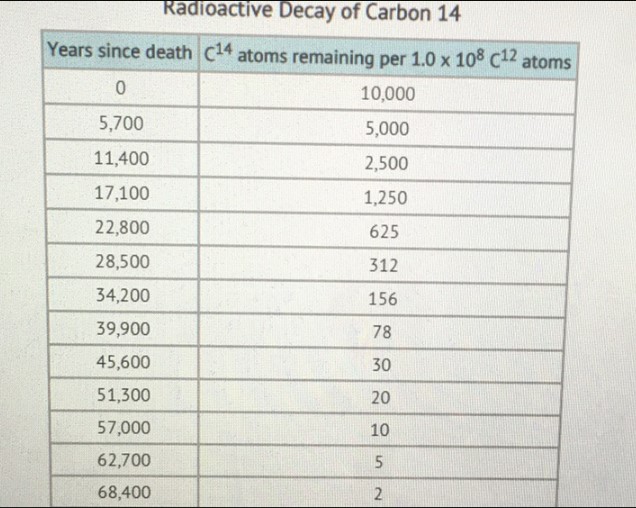
Use the chart to determine the half-life of carbon- 14
A) 5,000 years
B) 5,700 years
C) 10,000 years
D) 11,400 years
# Radioactive Decay of Carbon 14
| Years since death | $\mathrm{C}^{14}$ atoms remaining per $1.0 \times 10^{8} \mathrm{C}^{12}$ atoms |
| --- | --- |
| 0 | 10,000 |
| 5,700 | 5,000 |
| 11,400 | 2,500 |
| 17,100 | 1,250 |
| 22,800 | 625 |
| 28,500 | 312 |
| 34,200 | 156 |
| 39,900 | 78 |
| 45,600 | 30 |
| 51,300 | 20 |
| 57,000 | 10 |
| 62,700 | 5 |
| 68,400 | 2 |
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1: Identify the half-life of carbon- 14 from the table.
The half-life of a radioactive isotope is the time it takes for the number of atoms to decrease by half. From the table, we can see that it takes 5,700 years for the number of carbon- 14 atoms to decrease from 10,000 to 5,000 per 1.0 × 10^8 C^12 atoms. This means that 5,700 years is the half-life of carbon- 14.
Step 2: Verify the half-life by observing the next decrease in the table.
To confirm that 5,700 years is indeed the half-life, we can check the next data point. It takes 11,400 years for the number of carbon- 14 atoms to decrease from 10,000 to 2,500 per 1.0 × 10^8 C^12 atoms. This is a decrease by half from the previous data point, which further supports the half-life of 5,700 years.
Final Answer
The half-life of carbon- 14 is 5,700 years (Option B).
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students