QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
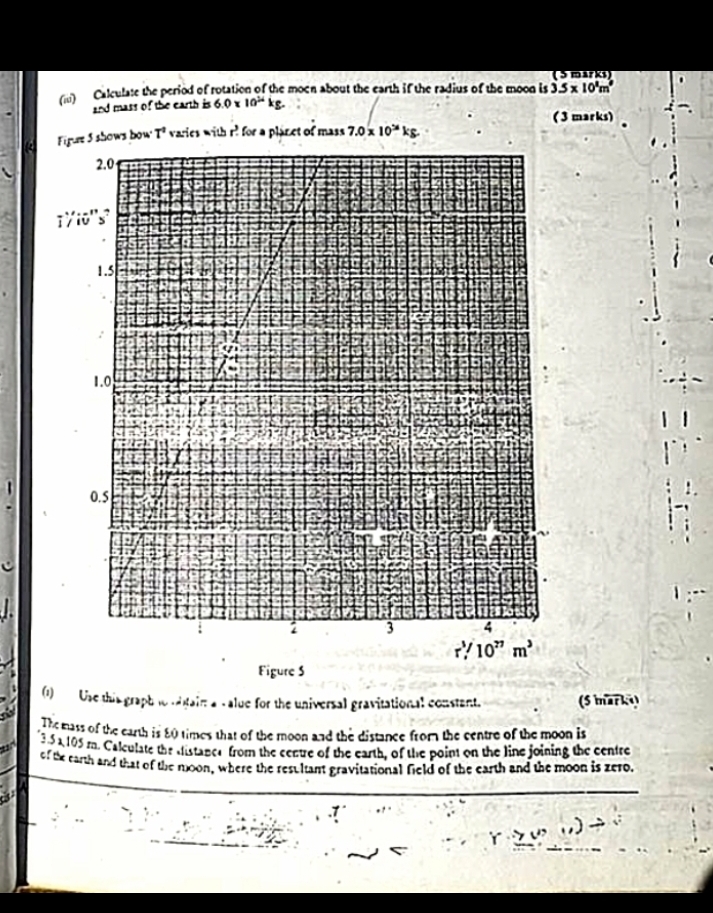
s Caleutate the period of rotation of the mocn about the earth if the radius of the mooa ks 3.5 x 10°’ 2
. (6) as of te cath B 60 10g. J
: : 7 : Gorka | AT
k pee shows bow T' vas wi for a placet of mass 70 10% ks. I ; ba
WEEE EET ET 1
| ma
Jn Ggssias AMHR; BRBELEE ARLHS RY SLLn Tan i
Wl EERE eee EE in
EnnbaETS^4 Eesspragann Riis i
- ASE ARES EEbqcnaEsnusiay td
ol SAE EE ERR Aaaus {
A Er EE rr rr eR \
SOERSREA^7NRRFo Ean GER RRA RID IL a
| TE Fir eat Eh 8
Emus BabeRang =r
Bf HODES MENT = ead i
| EEE SHE PEE EEE fl 3 Ex
| 10EEEE = =e 2
| CEs ne
agin le (|
i di 3 re Ge CRE me
seabyagsndEsoatns guat baleen Edy |
NN EE i
dA Ah MTD RRS RE 5 Rah 1nd
i FR CE RR Rh niga i
{ [ELH Ere] Fe] Daf el erm iy 24
3 i Hina fhaneti SEED 2
| FEaEN CERES = FREER -
! cerns HE AH ER =
I FEE Fr EE ER REE ;
J ) #107 m !
7 Figwes
© Ure hingng w stair a aloe for the universal gravitation coaster. Lo (wana
Tote ah is £0 times that of the moon aad the distance fron the centre of he moon is
lee carts Calulate te istazc from the cere of the cart, of the point on the line joining be centre
: [and Gatol the moon, where the result gravitation] field of the earth and the mooa fs zevo. c
] —_— LONE
i Bri ons © eit IO \
rT WE AAI SU
Attachments
2 days agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1I.
g_{resultant} = g_{Earth} + g_{moon} = 2.68 \times 10^{-3} \text{ m/s}^2 + 1.58 \times 10^{-5} \text{ m/s}^2 = 2.69 \times 10^{-3} \text{ m/s}^2
Understanding the Problem The problem asks us to calculate the period of rotation of the moon about the Earth, given the radius of the moon's orbit as 3.5 x 10^6 km and the mass of the Earth as 60 x 10^24 kg. II. Calculating the Period of Rotation To calculate the period of rotation, we can use Kepler's Third Law, which states that the square of the period of a planet is proportional to the cube of the semi-major axis of its orbit. The formula for Kepler's Third Law is: First, we need to convert the radius of the moon's orbit from kilometers to meters: III. Calculating the Period of Rotation (continued) Therefore, the period of rotation of the moon about the Earth is approximately 5.43 million seconds. IV. Calculating the Resultant Gravitation Field The problem also asks us to calculate the resultant gravitation field of the Earth and the moon at a point on the line joining the centers of the Earth and the moon. The formula for the gravitational field of a spherical body is: The gravitational field of the Earth is: The gravitational field of the moon is: V. Calculating the Resultant Gravitation Field (continued) Assuming the mass of the moon is 7.35 x 10^22 kg and the distance from the center of the moon is 3.85 x 10^8 m, we can calculate the gravitational fields of the Earth and the moon: Therefore, the resultant gravitational field is: VI.
Final Answer
The period of rotation of the moon about the Earth is approximately 5.43 million seconds. The resultant gravitational field of the Earth and the moon at a point on the line joining the centers of the Earth and the moon is approximately 2.69 x 10^- 3 m/s^2.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students