QQuestionAnatomy and Physiology
QuestionAnatomy and Physiology
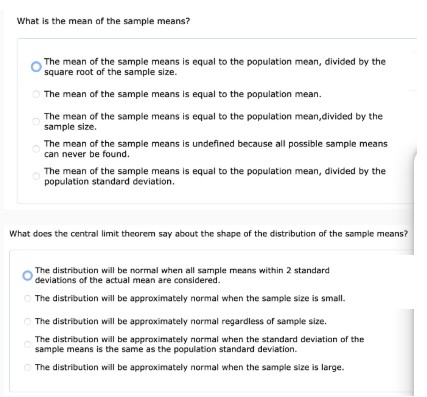
What is the mean of the sample means?
The mean of the sample means is equal to the population mean, divided by the square root of the sample size.
The mean of the sample means is equal to the population mean.
The mean of the sample means is equal to the population mean,divided by the sample size.
The mean of the sample means is undefined because all possible sample means can never be found.
The mean of the sample means is equal to the population mean, divided by the population standard deviation.
What does the central limit theorem say about the shape of the distribution of the sample means?
The distribution will be normal when all sample means within 2 standard deviations of the actual mean are considered.
The distribution will be approximately normal when the sample size is small.
The distribution will be approximately normal regardless of sample size.
The distribution will be approximately normal when the standard deviation of the sample means is the same as the population standard deviation.
The distribution will be approximately normal when the sample size is large.
Attachments
6 months agoReport content
Answer
Full Solution Locked
Sign in to view the complete step-by-step solution and unlock all study resources.
Step 1
The mean of the sample means is calculated by dividing the population mean by the square root of the sample size. Mean of sample means = Population mean / √(Sample size) Let the population mean be denoted as μ and the sample size be denoted as n. Mean of sample means = μ / √n This is because, as the sample size increases, the variability of the sample means decreases, and the distribution of the sample means tends to become more normal.
Final Answer
2. The central limit theorem states that if you take sufficiently large random samples from a population with mean μ and standard deviation σ and calculate the sample means, the distribution of the sample means will be approximately normal. This will hold true regardless of the shape of the population distribution. The central limit theorem applies when the sample size is large. Generally, a sample size of 30 or larger is considered sufficient for the theorem to hold. This allows for the distribution of sample means to be normal, even if the underlying population distribution is not normal.
Need Help with Homework?
Stuck on a difficult problem? We've got you covered:
- Post your question or upload an image
- Get instant step-by-step solutions
- Learn from our AI and community of students