Page 1
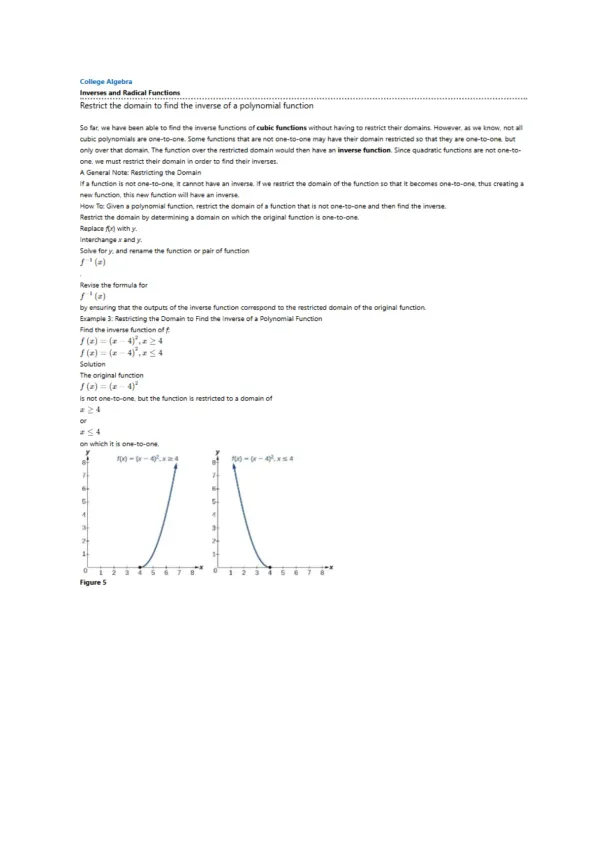
Loading page image...
Page 2

Loading page image...
Page 3
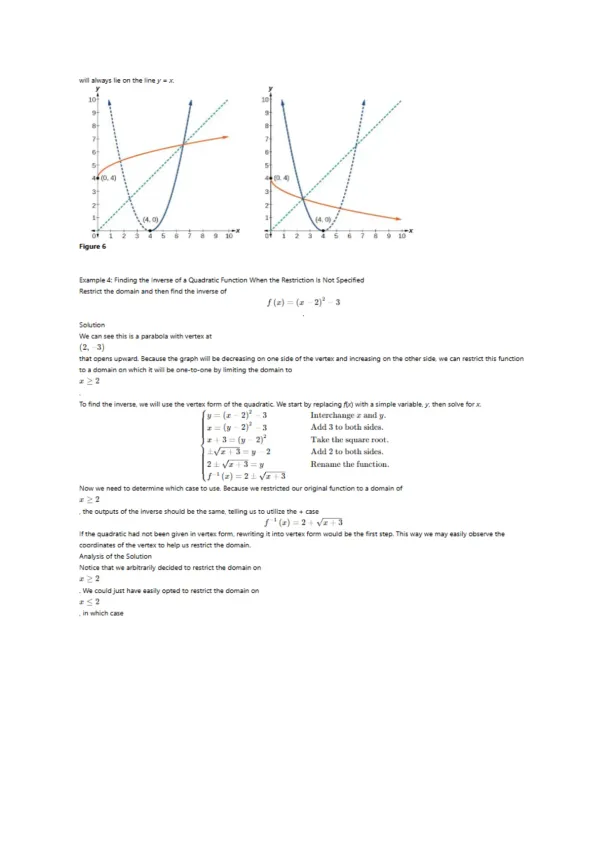
Loading page image...
Learn how to find the inverse of a polynomial function by restricting its domain. This lesson in College Algebra covers inverse functions and radical functions with practical examples to help you understand and apply the concepts.
Loading page image...
Loading page image...
Loading page image...
This document has 7 pages. Sign in to access the full document!