Solution Manual for Discrete Mathematics (Classic Version), 5th Edition

Preview (31 of 135 Pages)

100%

Purchase to unlock

Loading page image...

DISCRETEMATHEMATICSFIFTHEDITIONJohn A. DosseyIllinois State UniversityAlbert D. OttoIllinois State UniversityLawrence E. SpenceIllinois State UniversityCharles Vanden EyndenIllinois State UniversityINSTRUCTOR’SSOLUTIONSMANUAL

Loading page image...

Contents1An Introduction to Combinatorial Problems and Techniques11.1The Time to Complete a Project . . . . . . . . . . . . . . . . . . . . . . . . .11.2A Matching Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .41.3A Knapsack Problem. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .41.4Algorithms and Their Efficiency. . . . . . . . . . . . . . . . . . . . . . . . .4Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . .52Sets, Relations, and Functions62.1Set Operations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .62.2Equivalence Relations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .72.3Partial Ordering Relations. . . . . . . . . . . . . . . . . . . . . . . . . . . .82.4Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .102.5Mathematical Induction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .112.6Applications. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . .123Coding Theory143.1Congruence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .143.2The Euclidean Algorithm. . . . . . . . . . . . . . . . . . . . . . . . . . . . .153.3The RSA Method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .173.4Error-Detecting and Error-Correcting Codes. . . . . . . . . . . . . . . . . .173.5Matrix Codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .183.6Matrix Codes That Correct All Single-Digit Errors . . . . . . . . . . . . . . .19Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . .20iii

Loading page image...

Table of Contents4Graphs224.1Graphs and Their Representations . . . . . . . . . . . . . . . . . . . . . . . .224.2Paths and Circuits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .244.3Shortest Paths and Distance. . . . . . . . . . . . . . . . . . . . . . . . . . .274.4Coloring a Graph. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .284.5Directed Graphs and Multigraphs. . . . . . . . . . . . . . . . . . . . . . . .30Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . .345Trees365.1Properties of Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .365.2Spanning Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .385.3Depth-First Search . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .405.4Rooted Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .425.5Binary Trees and Traversals . . . . . . . . . . . . . . . . . . . . . . . . . . . .465.6Optimal Binary Trees and Binary Search Trees . . . . . . . . . . . . . . . . .51Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . .606Matching636.1Systems of Distinct Representatives. . . . . . . . . . . . . . . . . . . . . . .636.2Matchings in Graphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .636.3A Matching Algorithm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .666.4Applications of the Algorithm. . . . . . . . . . . . . . . . . . . . . . . . . .666.5The Hungarian Method. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .67Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . .677Network Flows687.1Flows and Cuts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .687.2A Flow Augmentation Algorithm . . . . . . . . . . . . . . . . . . . . . . . . .707.3The Max-Flow Min-Cut Theorem. . . . . . . . . . . . . . . . . . . . . . . .737.4Flows and Matchings. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .74Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . .75iv

Loading page image...

Table of Contents8Counting Techniques788.1Pascal’s Triangle and the Binomial Theorem. . . . . . . . . . . . . . . . . .788.2Three Fundamental Principles. . . . . . . . . . . . . . . . . . . . . . . . . .788.3Permutations and Combinations. . . . . . . . . . . . . . . . . . . . . . . . .798.4Arrangements and Selections with Repetitions. . . . . . . . . . . . . . . . .798.5Probability. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .808.6The Principle of Inclusion-Exclusion . . . . . . . . . . . . . . . . . . . . . . .818.7Generating Permutations andr-Combinations. . . . . . . . . . . . . . . . .82Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . .829Recurrence Relations and Generating Functions849.1Recurrence Relations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .849.2The Method of Iteration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .889.3Linear Difference Equations with Constant Coefficients. . . . . . . . . . . .919.4∗Analyzing the Efficiency of Algorithms with Recurrence Relations. . . . . .949.5Counting with Generating Functions . . . . . . . . . . . . . . . . . . . . . . .999.6The Algebra of Generating Functions. . . . . . . . . . . . . . . . . . . . . . 100Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10210Combinatorial Circuits and Finite State Machines10510.1Logical Gates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10510.2Creating Combinatorial Circuits. . . . . . . . . . . . . . . . . . . . . . . . . 10710.3Karnaugh Maps. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10910.4Finite State Machines. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115v

Loading page image...

Table of ContentsAppendices120A An Introduction to Logic and Proof120A.1Statements and Connectives. . . . . . . . . . . . . . . . . . . . . . . . . . . 120A.2Logical Equivalence. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121A.3Methods of Proof . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125Supplementary Exercises. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127B Matrices130vi

Loading page image...

Chapter1An Introduction toCombinatorial Problemsand Techniques1.1THE TIME TO COMPLETE A PROJECT2.31; A-B-E-G4.39; A-C-G-H6.16; B-D-F-H8.27; A-D-E-H10.27; A-B-D-G1

Loading page image...

Chapter1An Introduction to Combinatorial Problems and Techniques12.29; C-F-I14.33; H-I-F-G16.31; D-E-I18.20 minutes2

Loading page image...

1.2A Matching Problem1.2A MATCHING PROBLEM2.7204.2106.848.168010.19,958,40012.1814.504016.12618.21020.11922.132024.504026.24028.12001.3A KNAPSACK PROBLEM2.T4.F6.F8.F10.T12.T14.T16.no18.yes; 3220.∅,{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}; 1622.12824.102426.25628.2630.{1,4,6,7,8,9,10,11,12}1.4ALGORITHMS AND THEIR EFFICIENCY2.yes; 04.no6.no8.−1, 9, 84; 3, 17, 8410.−4,−4, 41, 95; 2, 11, 33, 9512.11100014.0010103

Loading page image...

Chapter1An Introduction to Combinatorial Problems and Techniques16.kja1a2a3311121111111011118.kja1a2a3a441110111120.The circled numbers in the table below indicated the items being compared.22.The circled numbers in the table below indicated the items being compared.24.6.5 years, 2.7 seconds26.2.3×1010years, 12.5 seconds4

Loading page image...

Chapter 1Supplementary Exercises28.4n−330.3n−232.−4,−4, 41, 95SUPPLEMENTARY EXERCISES2.20; B-E-F-H4.3366.408.1404010.T12.F14.T16.T18.1620.no22.yes; 024.−5, 7, 7, 8826.∅,{4},{3},{3,4},{2},{2,4},{2,3},{2,3,4},{1},{1,4},{1,3},{1,3,4},{1,2},{1,2,4},{1,2,3},{1,2,3,4}28.4.92×108years30.432.4r−35

Loading page image...

Chapter2Sets, Relations, andFunctions2.1SET OPERATIONS2.A∪B={1,2,4,5,6,7,9},A∩B={1,4,6,9},A−B=∅,A={2,3,5,7,8}, andB={3,8}4.A∪B={2,3,4,5,6,7,8,9},A∩B={7,9},A−B={3,4,6,8},A={1,2,5}, andB={1,3,4,6,8}6.{(3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3)}8.{(p, a),(p, c),(p, e),(q, a),(q, c),(q, e),(r, a),(r, c),(r, e),(s, a),(s, c),(s, e)}10.12.ABABC14.A={1, 2},B={1, 3}, andC={1}16.A={1, 2},B={1, 3}, andC={1}6

Loading page image...

2.2Equivalence Relations18.A20.∅22.A∩B24.A∪B26.The equalityA−B=B−Aholds if and only ifA=B.28.The equalityA∩B=Aholds if and only ifA⊆B.2.2EQUIVALENCE RELATIONS2.reflexive and symmetric4.reflexive, symmetric, and transitive6.reflexive and symmetric8.none10.reflexive and symmetric12.reflexive and transitive14.The equivalence class ofRcontaining ABCD consists of the string ABC and thestrings of 4 letters having A as their first letter and C as their third letter. There are262= 676 distinct equivalence classes ofR.16.The equivalence class ofRcontaining{1, 2, 3}is the set containing the followingfour elements ofS:{1, 3},{1, 2, 3},{1, 2, 3, 4}, and{1, 3, 4}. There are 8 differentequivalence classes ofR, namely the sets consisting of the elementsS,S∪ {2},S∪ {4},andS∪ {2,4}for everyS⊆ {1,3,5}.18.The equivalence class ofRcontaining (5,8) is the set{(x1, x2) : eachxiis an integer andx1−x2= 5−8}.There are infinitely many distinct equivalence classes ofR, namely, the sets of theform{(x1, x2) : eachxiis an integer andx1−x2=k},wherek= 0,±1,±2,±3, . . ..20.{(1,1),(1,3),(1,6),(3,1),(3,3),(3,6),(6,1),(6,3),(6,6),(2,2),(2,5),(5,2),(5,5),(4,4)}24.The equivalence classes have the formE1×E2, whereEiis an equivalence class ofRi.28.There are 5 partitions of a set with three elements.32.LetSbe a nonempty set andRan equivalence relation onS. Then there is a functionfwith domainSsuch thats1R s2if and only iff(s1) =f(s2).7

Loading page image...

Chapter2Sets, Relations, and Functions2.3PARTIAL ORDERING RELATIONS2.not antisymmetric4.partial ordering6.not antisymmetric8.not antisymmetric10.134212.{1, 2, 3, 4}{3, 4}{1, 2}{1, 3}{1, 4}{2, 3}{2, 4}14.R={(a, a),(b, b),(b, a),(c, c),(c, b),(c, a),(d, d),(d, a)}16.R={(1,1),(2,2),(2,1),(2,4),(4,4),(8,8),(8,4)}18.The maximal elements are{1},{2}, and{3}; the only minimal element is{1, 2, 3}.20.The only minimal element is 0; there are no maximal elements.22.One possible sequence is 1, 3, 2, 4.24.One possible sequence is 1, 3, 2, 6, 4, 12.26.LetSdenote the set of residents of Illinois andRbe defined so thatx R ymeans thatxis a sister ofy.28.Every prime integer is a minimal element; there are no maximal elements.30.(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4)8

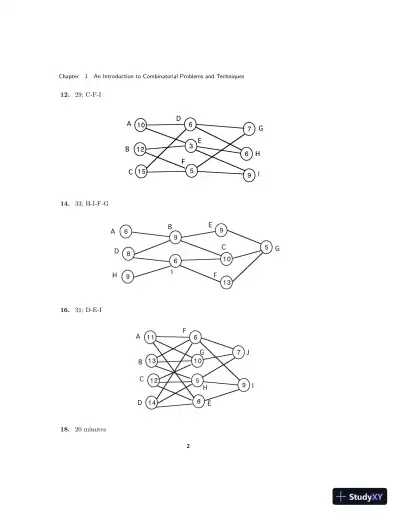
Loading page image...

2.3Partial Ordering Relations32.(9, 4)(9, 2)(8, 4)(8, 2)(7, 4)(7, 2)(9, 6)(9, 3)(8, 6)(8, 3)(7, 6)(7, 3)36.(a)Suppose thatyis element ofSsuch thatx R yis false. If there is no elementy1inSsuch thaty1R y, thenyis a minimal element ofS, contradicting thatxis the unique minimal element ofS. Thus there must be such an elementy1. Ifthere is no elementy2inSsuch thaty2R y1, theny1is a minimal element ofS,another contradiction. So there must be such an elementy2. BecauseSis finite,continuing in this manner must produce a minimal elementykofSdifferent fromx. Becausexis the unique minimal element ofS, the assumption that there isan elementyofSsuch thatx R yis false must be incorrect. Thusx R sis truefor everys∈S.(b)LetZdenote the set of integers andS=Z∪ {∅}. LetRbe the relation definedonSbyx R yif and only if one of the following holds: (i)x, y∈Zandx≤y, or(ii)x=y=∅. Then∅is the unique minimal element inS, but∅R zis falsefor everyz∈Z.40.2n42.2n·3n(n−1)/29

Loading page image...

Chapter2Sets, Relations, and Functions2.4FUNCTIONS2.not a function with domainX4.a function with domainX6.a function with domainX8.a function with domainX10.a function with domainX12.not a function with domainX14.416.1318.820.722.−124.626.−228.1030.0.7832.6.6434.3.2236.−2.5638.gf(x) =g(f(x)) =√x2+ 1 andf g(x) =f(g(x)) =x+ 140.gf(x) =13xandf g(x) = 3x42.gf(x) = 5(2x)−22xandf g(x) = 25x−x244.gf(x) = 4x−12−xandf g(x) = 3x−23−x46.one-to-one and onto48.neither one-to-one nor onto50.one-to-one but not onto52.onto but not one-to-one54.f−1(x) =x+ 2356.f−1(x) does not exist.58.f−1(x) does not exist.60.f−1(x) =3√x+ 162.ForY={x∈X:x= 0}, we haveg−1(x) =−1x.64.Ifn < m, there are no one-to-one functions; and ifm≤n, there areP(n, m) =n(n−1)(n−2)· · ·(n−m+ 1)one-to-one functions.68.LetX={1},Y={2,3}, andZ= 4. Definef:X→Ybyf(x) = 2 for allx∈Xandg:Y→Zbyg(y) = 4 for ally∈Y.10

Loading page image...

2.5Mathematical Induction2.5MATHEMATICAL INDUCTION2.7, 9, 13, 21, 37, 694.xn={xifn= 1x·xn−1ifn≥26.Letxndenote thenth odd positive integer. Thenxn={1ifn= 1xn−1+ 2ifn≥2.8.Ifk= 1, the sets{x1, x2, . . . , xk}and{x2, x3, . . . , xk+1}are disjoint.10.Ifk= 0, the induction hypothesis cannot be applied toak−1.28.s0+s1+· · ·+sn= (n+ 1)(s0+nd2)2.6APPLICATIONS2.564.9246.1208.71510.n12.r!14.3116.409618.12820.1522.3624.28626.12628.6444.There aren2+n+ 22regions.11

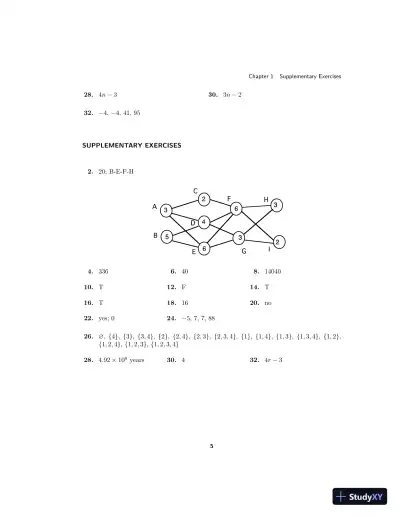
Loading page image...

Chapter2Sets, Relations, and FunctionsSUPPLEMENTARY EXERCISES2.{1,2,3,4,5}4.{1,2,4}.6.{1,2,4,5,6}8.{2,3}10.12.ABCABC14.gf(x) = 2(x3+ 1)−5 = 2x3−3 andf g(x) = (2x−5)3+ 1 = 8x3−60x2+ 150x−12416.not a function with domainX18.not a function with domainX20.neither one-to-one nor onto22.one-to-one and onto24.f−1does not exist.26.f−1=3√x−528.8430.21032.{1,7},{2,6},{3,5},{4},{8}34.the sets of positive and negative real numbers36.538.640.(b)a=±142.reflexive only48.x∨x=xfor allx∈S, 1∨y=y∨1 =yfor ally∈S, 2∨3 = 3∨2 = 6, 2∨4 = 4∨2 = 4,2∨6 = 6∨2 = 6, 3∨6 = 6∨3 = 6,x∨yis undefined in all other cases12

Loading page image...

Chapter 2Supplementary Exercises52.LetSdenote the set of all subsets of{1,2,3}that contain at most two elements, andletRbe the relation “is a subset of.”IfA={1},B={2}, andC={3}, thenA∨B={1,2},B∨C={2,3}, andA∨C={1,3}, but (A∨B)∨Cdoes not exist.54.[n] ={−n, n}56.f(x) =⎧⎨⎩xifx≡0 (mod 3)x−1ifx≡1 (mod 3)x−2ifx≡2 (mod 3)13

Loading page image...

Chapter3Coding Theory3.1CONGRUENCE2.The quotientqis 3, and the remainderris 0.4.q= 12 andr= 76.q=−4 andr= 178.q=−6 andr= 910.p≡q(modm)12.p≡q(modm)14.p≡q(modm)16.p≡q(modm)18.[5]20.[4]22.[2]24.[8]26.[3]28.[5]30.[3]32.[6]34.[1]36.[4]38.11A.M.40.542.344.February, March, and November46.[2] = [10] = [−6]; [7] = [39] = [−1] = [−17]; [45] = [−3]14

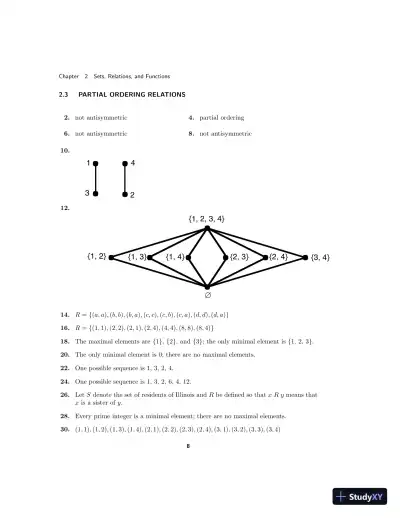
Loading page image...

3.2The Euclidean Algorithm48.InZ6, [2]= 0 and [3]= 0, but [2]·[3] = [0].50.(a)T6T5T8T7T9T4T3T2T1123457896134687151013(b)The whole project can be completed in 15 days.(c)The critical path isT1–T2–T4–T8.52.(b)Takea=14,b= 0,c= 1,x= 2,y= 0, andm= 2.3.2THE EUCLIDEAN ALGORITHM2.−54,−27,−18,−9,−6,−3,−2,−1,1,2,3,6,9,18,27,544.−24,−12,−8,−6,−4,−3,−2,−1,1,2,3,4,6,8,12,246.iri−13410217112429333140[Print 31]8.iri−1451014312221130[Print 11]15

Loading page image...

Chapter3Coding Theory10.iri−189055134221313485563728190[Print 1]12.3014.iqirixiyi−1203010089901122321−223203−3731294−9470−3170[Print 29, 4,−9]16.iqirixiyi−12311001820111491−12335−3431144−5427−111452026−33[Print 7,−11, 14]18.iqirixiyi−1555100214601105551023481−3131744−14637−27752058−15[Print 37,−27, 7]20.(a)yes(b)no22.(a)yes(b)yes24.x= 95,y=−13326.impossible16

Loading page image...

3.3The RSA Method3.3THE RSA METHOD2.10, 12, 144.46, 7, 156.QRr1r2pe13029141333033147018187311830183111830181011830180[Print 30]8.QRr1r2pe17532614974926130646413613779376301616311103410101100941000[Print 94]10.QRr1r2pe11210150114412144502505235232512159331110363026226231187111148711015970590[Print 70]12.12014.26416.518.1120.2122.7724.830.a=b= 2,x= 1,x′= 23.4ERROR-DETECTING AND ERROR-CORRECTING CODES2.04.16.08.010..941512..074614..004216..913517

Loading page image...

Chapter3Coding Theory18.120.522.224.626.110028.1011130.332.434.(a)12(b)636.(a)19(b)940.Let the message wordxbec11c12. . . c1sc21c22. . . c2s. . . cs1cs2. . . css.Choosebi= 0 orbi= 1 so thatci1ci2. . . cis+biis even fori= 1,2, . . . , s, and choosedk= 0 ordk= 1 so thatc1kc2k. . . csk+dkis even fork= 1,2, . . . , s. Let the codewordcorresponding toxbec11c12. . . c1sc21c22. . . c2s. . . cs1cs2. . . cssb1b2. . . bsd1d2. . . ds.This is an (s2, s2+ 2s)-block code in which the minimal distance between codewordsis at least 3.3.5MATRIX CODES2.644.10246.001111118.0111101010.11×712.13×614.71116.00000, 01111, 10011, 1110018.000000, 001011, 010110, 011101, 100101, 101110, 110011, 11100020.0000000, 0011101, 0101011, 0110110, 1000111, 1011010, 1101100, 111000122.24.⎡⎢⎢⎢⎢⎣101110100010001⎤⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣001011111100010001⎤⎥⎥⎥⎥⎥⎥⎦18

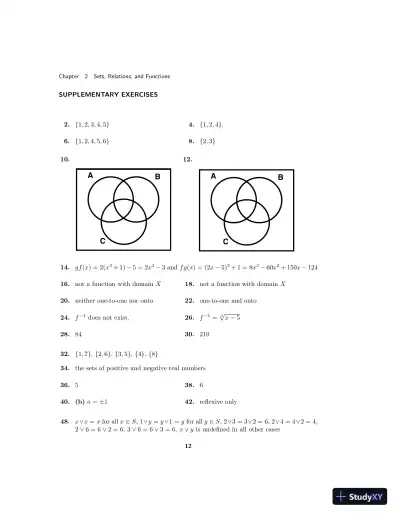
Loading page image...

3.6Matrix Codes That Correct All Single-Digit Errors26.28.⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣1001011001011000010000100001⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣1111011011011111000001000001000001000001⎤⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦30.⎡⎢⎢⎣10001001010001010010101000010110⎤⎥⎥⎦32.yes34.no, 110136.yes38.no, 101140.(a)The codewords determined byzandware [0 0 0 0 0 0 0 0] and [1 0 0 0 0 0 0 0];so the distance between these codewords is 1.(b)By Theorem 3.2(a), not all errors in a single digit can be detected.42.⎡⎢⎢⎣1000110010010100101110001011⎤⎥⎥⎦3.6MATRIX CODES THAT CORRECT ALL SINGLE-DIGIT ERRORS2.1001, 104.1100, ??6.0000, 108.0110, 0010.0000, 11112.0111, ??14.1000, 01116.1101, 11118.0000, 10120.0010, 00122.1111, ??24.1010, 10126.0000, 01028.0110, 01030.10, 01, 10, ??19

Loading page image...

Chapter3Coding Theory32.1434.3036.k= 26 andn= 3138.k= 1013 andn= 102340.(a)(1−p)4(b)(1−p)7+ 7p(1−p)6SUPPLEMENTARY EXERCISES2.true4.false6.[8]8.[3]10.1112.2 and 114.416.1518.4720.2 = 41a−76b22.47 = 6a+ 11b24.10, 6, 23, 2126.QRr1r2pe1251151312531521416421016161012525250[Print25]28.168030.1632.034..0000000557236.338.The minimal Hamming distance between codewords cannot exceed the number of 1sin the codeword containing the fewest 1s.40.2k42.C(n,0) +C(n,1) +· · ·+C(n, s).44.00101111146.0000, 0111, 1000, 111120

Loading page image...

Chapter 3Supplementary Exercises48.50.⎡⎢⎢⎢⎢⎢⎢⎢⎢⎣111111100000010000001000000100000010000001⎤⎥⎥⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣100010111000011100011000001000001000001000001⎤⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦52.⎡⎢⎢⎣100001100010010001001000111000110011⎤⎥⎥⎦54.0111, 11056.0101, ??58.1101, ??60.1011, 01062.(a)57×63(b)63×664.566.1, 2, 4, 8, 16, 32, and 64 pounds68.No; considera= 4,b= 2, andc= 8.21

Loading page image...

Chapter4Graphs4.1GRAPHS AND THEIR REPRESENTATIONS2.V={F, G, H};E={{F, G}}4.V={A, B, C, D};E={{A, C},{A, D},{B, C},{B, D}}6.8.WXYZABYX10.no12.yes14.no18.1234567891022

Loading page image...

4.1Graphs and Their Representations20.none, 0;C, 124.no26.⎡⎢⎢⎣0111101111011110⎤⎥⎥⎦V1:V2, V3, V4V2:V1, V3, V4V3:V1, V2, V4V4:V1, V2, V328.⎡⎢⎢⎣0111101011011010⎤⎥⎥⎦V1:V2, V3, V4V2:V1, V3V3:V1, V2, V4V4:V1, V330.V1V2V3V4V532.V3V1V4V5V234.There are no edges.36.no42.(a)yes(b)no(c)no44.23

Loading page image...

Chapter4Graphs46.48.[2,3][2,4][1,3][1,4][3,4][1,2]50.n52.the vertices corresponding to primespsuch thatp > n24.2PATHS AND CIRCUITS2.not a graph4.a graph6.parallel edges:a, b, c; loops:f8.parallel edges: none; loops: none10.(a)e(1);b, c(2);a, f, b, a, d(5)(b)e(1);a, d(2);b, c(2);a, f, c(3);b, f, d(3)(c)e;b, c;a, d(d)a, b, c, d(4);a, e, c, f(4);b, f, d, e(4);a, d, e(3);c, d, f(3);b, c, e(3);a, b, f(3)24

Loading page image...

4.2Paths and Circuits12.no14.yes16.no18.no20.yes;a, g, d, e, h, b, c, i, f22.no24.yes,a, b, h, i, m, k, e, d, f, j, g, c26.no28.no30.no32.yes34.yes36.no38.no40.1, 2, 3, 4, 5, 13, 12, 11, 10, 9, 8, 7, 6, 16, 17, 18, 19, 20, 14, 15, 142.0000, 0001, 0011, 0010, 0110, 0111, 0101, 0100, 1100, 1101, 1111, 1110, 1010, 1011,1001, 100044.25

Preview Mode

This document has 135 pages. Sign in to access the full document!

Report

Study Now!

Document Details

Related Documents

AP Calculus AB Scoring Guide Unit 6 Progress Check

Clinical Psychologist

Module 4 Matrices

MATH 1324 Homework 5 Answers

Ap progress 1 5 all 5

The Fundamental Theorem of Calculus and Definite I

AP Calculus AB Scoring Guide

Investigating the Rising Cost of MTA Transit Fare

Module 11 Geometry

AP Calculus AB Unit 5 Progress Check Scoring Guide

Company

Explore

Study Tools